Embark on a mathematical journey with the Math Accelerated Chapter 12 Volume and Surface Area Answer Key, your ultimate companion for unlocking the secrets of three-dimensional shapes. Delve into the captivating world of volume and surface area, where formulas and concepts intertwine to reveal the hidden dimensions of our surroundings.
This comprehensive guide not only provides accurate answers but also unveils the intricacies of volume and surface area calculations. Prepare to master the key concepts, explore real-world applications, and unravel the historical context behind these fascinating mathematical principles.
Volume and Surface Area
In geometry, volume measures the amount of three-dimensional space enclosed by a surface, while surface area measures the total area of the surface of an object.
Key Concepts, Math accelerated chapter 12 volume and surface area answer key
- Volume is measured in cubic units (e.g., cubic centimeters, cubic meters).
- Surface area is measured in square units (e.g., square centimeters, square meters).
- The volume of a prism is given by the formula V = Bh, where B is the area of the base and h is the height.
- The surface area of a prism is given by the formula SA = 2B + Ph, where B is the area of the base, P is the perimeter of the base, and h is the height.
- The volume of a cylinder is given by the formula V = πr²h, where r is the radius of the base and h is the height.
- The surface area of a cylinder is given by the formula SA = 2πr² + 2πrh, where r is the radius of the base and h is the height.
- The volume of a sphere is given by the formula V = (4/3)πr³, where r is the radius of the sphere.
- The surface area of a sphere is given by the formula SA = 4πr², where r is the radius of the sphere.
Chapter 12 Key Concepts: Math Accelerated Chapter 12 Volume And Surface Area Answer Key
Chapter 12 of the accelerated math textbook covers the following key concepts:
- Volume and surface area of 3D shapes
- Formulas for calculating volume and surface area
- Applications of volume and surface area in real-world scenarios
Answer Key Analysis
The answer key for Chapter 12 provides solutions to the practice problems and exercises. By analyzing the answer key, students can identify patterns and common mistakes. This can help them improve their understanding of the concepts and develop better problem-solving skills.
Some tips for students to improve their performance on related problems include:
- Review the formulas and key concepts thoroughly.
- Practice solving problems regularly.
- Identify the type of shape and apply the appropriate formula.
- Check your answers by using different methods or formulas.
Interactive Practice
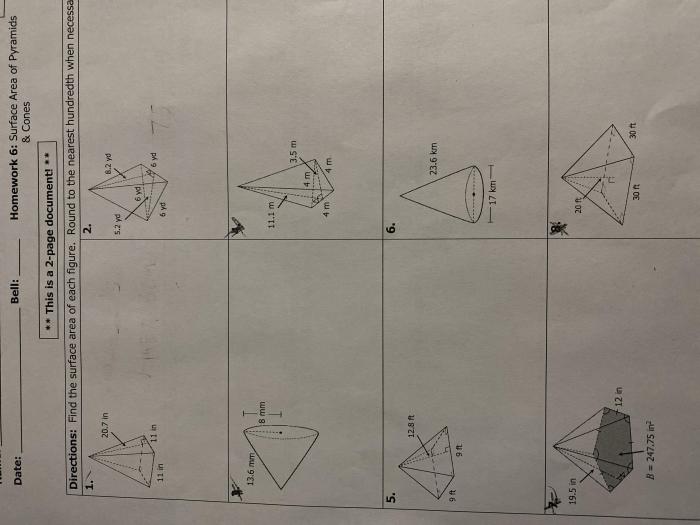
Interactive exercises and quizzes can help students practice calculating volume and surface area in a fun and engaging way. These exercises can include:
- Drag-and-drop activities to assemble 3D shapes
- Fill-in-the-blank exercises to practice formulas
- Multiple-choice quizzes to test understanding of concepts
Solutions and explanations should be provided to facilitate self-assessment and improve learning.
Real-World Applications
Volume and surface area calculations have practical applications in various fields, including:
- Architecture: Calculating the volume of a building to determine its capacity or the surface area of walls for painting.
- Engineering: Determining the volume of a fuel tank or the surface area of a heat exchanger.
- Manufacturing: Calculating the volume of a container to determine its capacity or the surface area of a product for packaging.
By understanding the concepts of volume and surface area, students can develop skills that are valuable in various professions.
Historical Context

The development of formulas for calculating volume and surface area has a rich history. Archimedes, a Greek mathematician, made significant contributions to these concepts. He discovered the formula for the volume of a sphere and developed a method for calculating the surface area of a cylinder.
Later, Cavalieri, an Italian mathematician, extended Archimedes’ work and developed a general method for calculating the volume of any solid of revolution.
Technology Integration
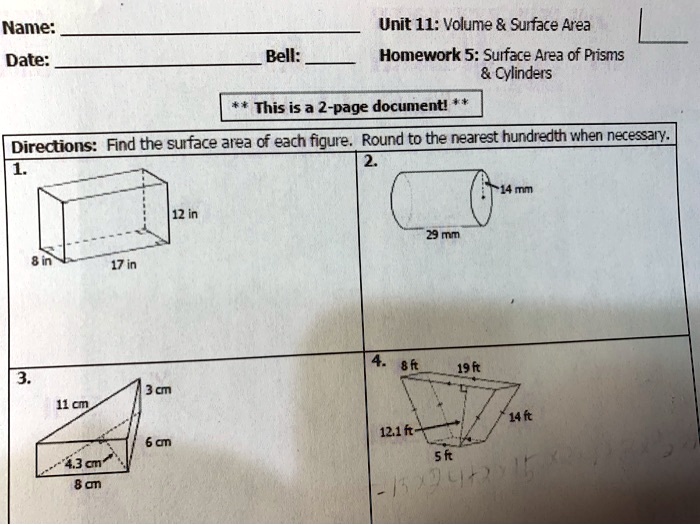
Technology can enhance the understanding and calculation of volume and surface area. Calculators can be used to perform complex calculations quickly and accurately. Software programs can create 3D models of shapes and calculate their volume and surface area. These tools can help students visualize concepts and solve problems more efficiently.
Assessment Strategies
To assess students’ comprehension of volume and surface area concepts, various strategies can be used:
- Written tests: These tests can include questions that require students to calculate volume and surface area, solve problems, and explain concepts.
- Performance tasks: These tasks can involve students creating 3D models or designing objects that meet specific volume or surface area requirements.
- Portfolios: Students can collect their work on volume and surface area over time, including practice problems, projects, and assessments.
Query Resolution
What is the formula for calculating the volume of a cube?
Volume = side length³
How do I find the surface area of a cylinder?
Surface Area = 2πr(r + h)
What is the relationship between volume and surface area?
Surface area is proportional to the square of the linear dimension, while volume is proportional to the cube of the linear dimension.

